Chapter 13. Merger Probability

Home - Welcome
Forum *(new)*
Lectures
1	A Word of Encouragement
2	Dar al-Hikma
3	Proclus' Elements
4	Reversion in the Corporeal
5	Mathematical Recursion
6	Episodic Memory
7	Mortality
7s	Classical Mortality Arguments
8	Personal Identity 1 2 3 4
9	Existential Passage 1 2 3
10	Precedent at Dar al-Hikma
10s	Images of Dar al-Hikma
11	Passage Types
12	A Metaphysical Grammar
13	Merger Probability
14	Ex Nihilo Probability
15	Noetic Reduction
16	Summary of Mathematical Results
17	Application to Other Species 1 2 3 4
18	Potential Benefits
19	A Dedication
Appendices
Works Cited
E-mail the author. E-mail the webmaster.
.

Chapter 13
Merger Probability

In Chapter 11 I drew out the passage types implicit in the concept of existential passage. One of those types — split passage — I view unlikely, perhaps even impossible. The same is not true of merged passage.

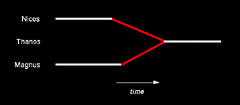
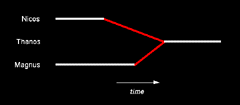
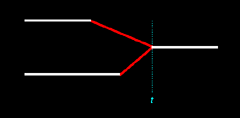
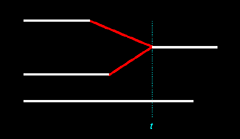
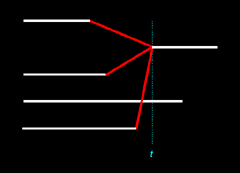
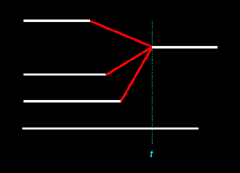
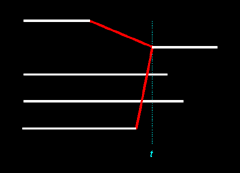
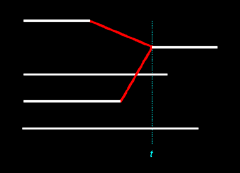
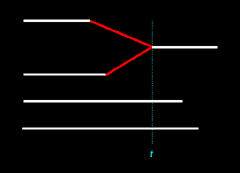
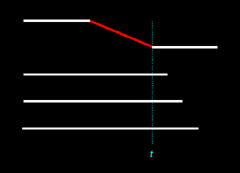
Let's consider two similar illustrations below. Each illustration represents an inferred two-to-one merger of Nicos and Magnus to Thanos.

Fig. 13.1

Fig. 13.2

The timelines in Figure 13.2 are altered slightly in relation to Figure 13.1. In Figure 13.2 Nicos' death has hastened somewhat, and Magnus' has tarried. The merged passage is still inferred because both Nicos and Magnus still pass away before the birth of Thanos. We can see from this example that merged passages, unlike split passages, are resilient against small changes in timing.

By the same reasoning we can deduce that one-to-one, or unitary, passages are likewise robust: they, too, are resilient against small changes in timing.

And so both unitary and merged passages would seem to be common. But how common? Would persons experience unitary passages more frequently than mergers? Or, instead, would they pass through mergers more frequently?

The question may appear intractable at first. Certainly, participants in existential passage cannot know what is happening to them. Nicos cannot know whether he participates in a unitary or merged passage. Neither can Thanos know if one, or many, or no passage participants transfer to his life. All participants must be ignorant of what transpires, as no knowledge of the event can reach their subjective viewpoints.

But it is here that an objective viewpoint again proves its value. Previously we've taken to the objective viewpoint only so that we might see the possible types of existential passage — unitary, merged, ex nihilo and split. The passage types became clear as we studied timeline illustrations representing a few Aegean idylls.

Now a question has arisen which cannot be answered by such isolated sketches. Something of a systematic, global view of the metaphysics is required if we are to learn just how common each passage type would be, relative to the others. This task requires that we abstract our objective viewpoint beyond the isolated sketches — refining it into a mathematical representation of the sketched events. The mathematics will supplant the illustrative method used so far. (Unfortunately the presentation of a mathematics must needs be quite dry, and for this dryness the author apologizes. Results are summarized in Chapter 16.)

We can think of the mathematics as our fourth stepping stone along the metaphysical path.

To ground the mathematics in reality, we should begin by recalling that Metaphysics by Default leans heavily upon naturalistic argument for support. Nicos passes to Thanos only if an indifferent Nature times events to their mutual advantage. Nature is the driving force. And Nature is, as Cicero has reminded us,[1] capricious in the allotment of destinies. "Capricious" we can read prosaically as "random."

Random events are individually unpredictable. But when conditions are stable, and populations are large, many types of random events "average out." And the resulting averages are predictable.

As example, we might consider the measurement of temperature: in, say, a glass of water. The temperature of each water molecule is random, unknowable. But the molecules distribute their individual temperatures about some average temperature. A thermometer dropped into the glass will tell us this average temperature with certainty.

In this chapter we are only concerned with averages: the average number of experienced merged passages, divided by the average number of experienced unitary passages. This quantity is formulated as a ratio. And the ratio can be found, provided that the timings of events are random.

Three approaches to the problem are possible. All three produce much the same solution. A summary of the several mathematical results will be presented in Chapter 16.

The first approach uses informal probability rules. This solution, being informal, is not entirely certain; but this method may be the most intuitive of the three. We'll walk through an informal probability solution within this chapter.

The second approach makes use of a "Monte Carlo program." The technique is akin to gamblers' odds-making: many random events are generated, and statistics are compiled on those events in order to ascertain the odds of each event type. Monte Carlo results will be presented in the summary of Chapter 16.

The third approach applies a formal probability calculus to the problem.[2] This technique is the most rigorous of the three, and its results may be considered a formal proof. In Chapter 16 we will compare the solution obtained by this formal probability calculus against the solutions obtained by the other two techniques. The text of the formal proof, which is rather difficult, I've relegated to Appendix A.

To start off, let's consider the first approach. With the help of informal probability rules we can find the experienced ratio of merged versus unitary passage.

We've already posited random timings. Two more preconditions must be added if the problem is to be mathematically tractable:

The population must be stable, neither increasing nor decreasing noticeably over time. Of course, each death decreases the population, and each birth increases it. But we must assume that these changes in population will cancel out over time, as the population maintains itself near some equilibrium size.

We assume, after Chapter 11, that split passages are rare. So we will disregard split passages in formulation of the mathematical problem.

Given these preconditions the mathematical problem can be solved. We open with the figure below:

Fig. 13.3
Unitary passage

Figure 13.3 illustrates a simple existential passage. It is a unitary passage, such as that experienced by Nicos and Thanos in the original version of the Aegean idyll. This will be the starting point of the solution by informal probability rules.

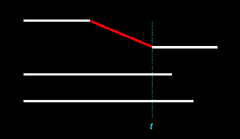
We'll "freeze" the timelines in Figure 13.3. These two timelines cannot be altered. For now they represent the only two lives which can have been extant in the idyllic cosmos. If we ask, "What is the probability that a unitary passage has occurred between them?" we see that the probability is frozen at 100%. It is certain. We can also express this certainty as a decimal probability. (Decimal probabilities range between 0 and 1, and they are a little easier to work with.) Expressed in this format, the probability of a unitary passage is equal to 1. Symbolically:

p₁ = 1

Here, p_nis the relative probability of an n-to-one passage, where n is to be understood as the number of persons "moving through" that passage. In this case, n = 1.

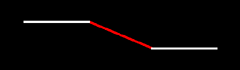
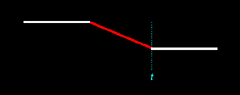
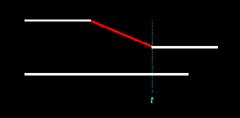
The passage occurs at the time of the conscious birth of the recipient, which is marked as time t in Figure 13.4 below:

Fig. 13.4
Unitary passage at time t

Time t is critical for this one particular passage. A person who passes away before time t participates in the passage. A person who passes away after time t does not. Time t is the sole criterion upon which the determination depends.

Keeping in mind the supposition that these two particular timelines are "frozen," we now add a third person to the figure. This third person is a contemporary of the first — which is to say, a contemporary of that person whom we've already committed to the existential passage. The new, third life will be random in duration. This person may pass away at any time, either before or after time t, unpredictably. 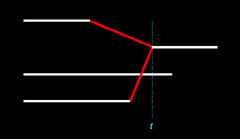The two possible types of outcomes are illustrated in the following two figures:

Fig. 13.5

Fig. 13.6

The addition of a third person opens up the possibility of a passage type which was not possible in Figure 13.4. Here we have our first opportunity for a two-to-one merged passage. As it happens, the first two-to-one merger is found in Figure 13.5. Merger occurs only in Figure 13.5; it does not occur in Figure 13.6. Since each of the two possible outcomes is equally likely, the probability of a two-to-one merger is here 1/2, or 0.5. Symbolically:

p₂ = 0.5

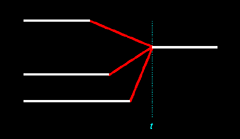
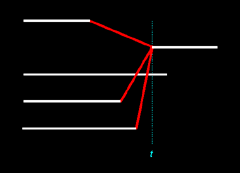
We can create another set of figures to determine the probability of a three-to-one merger. To do this we'll add a fourth person. Again, this additional person may pass away at any time, either before or after time t. Four types of outcomes are now possible:

Fig. 13.7

Fig. 13.8

Fig. 13.9

Fig. 13.10

Of these four figures, only Figure 13.7 contains a three-to-one merger. And so the probability of a three-to-one merger is here 1/4, or 0.25.

p₃ = 0.25

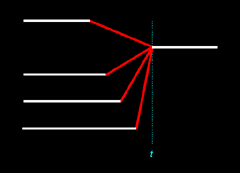
If we add a fifth person, we can determine the probability of a four-to-one merger. Adding this fifth person increases the number of possible outcomes to eight:

Fig. 13.11

Fig. 13.12

Fig. 13.13

Fig. 13.14

Fig. 13.15

Fig. 13.16

Fig. 13.17

Fig. 13.18

Of these eight figures, only Figure 13.11 contains a four-to-one merger. And so the probability of a four-to-one merger is here 1/8, or 0.125.

p₄ = 0.125

Relative probabilities for each passage type are emerging now, following the rule:

p_n = (1/2)^n-1 { n = 1 to infinity }

where, again, n is the number of persons passing through an n-to-one passage.

The first ten relative probabilities are tallied in Table 13.1:

Table 13.1
Relative passage probabilities

passage type

relative passage probability

1-to-1

1

2-to-1

0.5

3-to-1

0.25

4-to-1

0.125

5-to-1

0.0625

6-to-1

0.0313

7-to-1

0.0156

8-to-1

0.00781

9-to-1

0.00391

10-to-1

0.00195

We can see from these results that merged passages grow increasingly unlikely as the number of participants rises. This makes sense, as we have presupposed random timings.

Now we need to consider another important factor: the experiences of the persons involved in passage are at issue here, rather than the passages themselves.

Table 13.1 lists relative passage probabilities, but those probabilities are only a part of the finished solution. To get closer to the real solution we should think about the persons moving through the passages. Specifically, we note that:

1. In a unitary passage, one person passes through.
2. In a two-to-one merger, two persons pass through.
3. In a three-to-one merger, three persons pass through.
4. In a four-to-one merger, four persons pass through — and so on.

The importance of this observation is that although mergers grow increasingly unlikely as the number of participants increases, we must not lose sight of the corresponding fact that the number of participants is increasing apace. And these participants should be accounted for, if the calculated probabilities are to match up with their experiences. Another way of saying this is to point out that when a high-order, large-number merger occurs, many persons must perforce pass through it. That "aggregation" makes the merger more likely, from the standpoint of those involved, than the numbers of Table 13.1 would indicate.

The relative probabilities of each passage type, as experienced by the participants, can be calculated by multiplying the relative probability of the passage type by the number of persons involved in that passage. The modified probability formula becomes:

p_n = n x (1/2)^n-1

where, again, n is the number of persons involved in an n-to-one passage.

For a one-to-one unitary passage:

p₁ = 1 x (1/2)⁰= 1

For a two-to-one merger:

p₂ = 2 x (1/2)¹= 1

For a three-to-one merger:

p₃ = 3 x (1/2)²= 3/4 = 0.75

For a four-to-one merger:

p₄ = 4 x (1/2)³= 4/8 = 0.5

And so on. Table 13.2 summarizes the first ten of these relative experienced probabilities.

Table 13.2
Relative experienced probabilities

passage type

relative experienced probability

1-to-1

1

2-to-1

1

3-to-1

0.75

4-to-1

0.5

5-to-1

0.313

6-to-1

0.188

7-to-1

0.109

8-to-1

0.0625

9-to-1

0.0352

10-to-1

0.0195

This gets us closer to the real solution, but one more refinement remains. The probabilities in Table 13.2 are relative probabilities: that is to say, they are correctly proportioned, relative to one another. But they do not add up to 1 (i.e., 100%), which is what we should want of the absolute probabilities. Instead, we see that the first ten probabilities add up to 3.9772, which is larger than 1.

In order to convert these relative probabilities into absolute probabilities, it is necessary to find a normalizing constant,

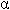, which, when divided into all the probabilities, makes them sum to 1 exactly. We can see that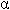

must be larger than 3.9772. Its exact value can be calculated by summing the relative experienced probabilities for all merger types, from n = 1 to n = infinity. The power series for this sum is: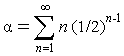

= 1 + 1 + 0.75 + 0.5 + 0.313 + 0.188 + 0.109 + ...

This sum is proved to be of the form: 1 / (1-x)². Here x = 1/2, so:

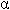= 4

For confirmation Appendix E sums the series mechanically, with same result.

This value of

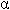, when divided into all the probabilities, makes them sum to 1 exactly. Hence they become the absolute experienced probabilities we've been seeking. So, dividing the relative experienced probability formula by 4, we get the formula for absolute experienced probability. Modifying our formula one last time, it becomes:

p_n = 0.25 n x (1/2)^n-1

Table 13.3 summarizes the first ten absolute experienced probabilities.

Table 13.3
Absolute experienced probabilities

passage type

absolute experienced probability

1-to-1

0.25

2-to-1

0.25

3-to-1

0.188

4-to-1

0.125

5-to-1

0.0781

6-to-1

0.0469

7-to-1

0.0273

8-to-1

0.0156

9-to-1

0.00879

10-to-1

0.00488

These probabilities can provide the solution to the problem. Restating and summarizing the original question:

What is the experienced ratio of merged versus unitary passage?

We can see in Table 13.3 that one-to-one unitary passages have an absolute experienced probability of 0.25, or 25%. We interpret this as meaning that a person should have a 25% chance of experiencing a unitary passage.[3]

All other passage probabilities sum to 75%. Since all other passages are merged passages, a person should have a 75% chance of experiencing a merged passage.

The ratio, 75:25, is just 3:1.

We conclude that the experienced ratio of merged versus unitary passage is 3:1. Under normal circumstances, a passage participant would be three times as likely to encounter a merged passage as a unitary passage.

In the next chapter we will determine the likelihood of ex nihilo passage.

next Chapter 14: Ex Nihilo Probability

Chapter 13 Endnotes

[1] As cited previously in Chapter 9, Section 3, note 15: "Nature is the one who has granted us the loan of our lives, without setting any schedule for repayment. What has one to complain of if she calls in the loan when she will?"

[2] The definitions and theorems of this calculus follow from John G. Kemeny and J. Laurie Snell, Finite Markov Chains (Princeton: D. Van Nostrand Company, 1960) 25, 35-39, 99-100. For additional references to these topics see William Feller, "Waiting Line And Servicing Problems," An Introduction to Probability Theory and Its Applications, 2 vols., 2^nd edition (New York: John Wiley & Sons, 1957) 413-21.

[3] It may be surprising to see that two-to-one mergers are just as likely to be encountered as one-to-one unitary passages. But the formula for absolute experienced probabilities correctly sets odds on both at 25%.