Chapter 6. Episodic Memory

Home - Welcome
Forum *(new)*
Lectures
1	A Word of Encouragement
2	Dar al-Hikma
3	Proclus' Elements
4	Reversion in the Corporeal
5	Mathematical Recursion
6	Episodic Memory
7	Mortality
7s	Classical Mortality Arguments
8	Personal Identity 1 2 3 4
9	Existential Passage 1 2 3
10	Precedent at Dar al-Hikma
10s	Images of Dar al-Hikma
11	Passage Types
12	A Metaphysical Grammar
13	Merger Probability
14	Ex Nihilo Probability
15	Noetic Reduction
16	Summary of Mathematical Results
17	Application to Other Species 1 2 3 4
18	Potential Benefits
19	A Dedication
Appendices
Works Cited
E-mail the author. E-mail the webmaster.
.

Chapter 6
Episodic Memory

The Church-Turing Thesis, abbreviated here as CT, applies recursive functions to common computing problems. Most of these problems are solved by "serial computers," which execute instructions in a linear sequence, one by one. CT also applies to computers which execute instructions in parallel, performing many computations concurrently. John Shepherdson[1] has proved the applicability of CT to parallel computers.[2]

Some parallel computer designs are inspired by the microscopic architecture of neural structures in the brain. Parallel computers known as "neural nets" are built so as to mimic these structures. Since we're chasing CT into the human body, it will be expedient to restrict pursuit of CT applications to neural nets alone.

In 1943 Warren McCulloch and Walter Pitts[3] designed a simple neural net which embodied only five physical rules.[4] They demonstrated that this simplistic neural net could perform all Turing machine computations. In 1995 Hava Siegelmann and Eduardo Sontag proved a more powerful conjecture, showing that all Turing machines can be simulated by neural nets of finite size.[5]

Recently neural nets have been refined so as to simulate the electrical "spiking" behavior common to real neurons. The spiking model places additional biological constraints on neural nets,[6] making modern versions more realistic than the early 40s model of McCulloch and Pitts. Like those early neural nets, spiking neural nets can also simulate all Turing machines effectively. In addition, Wolfgang Maas[7] has demonstrated that spiking neural nets can simulate other classes of machines, including finite automatons[8] and random access memory devices.[9] And very recently (1997) Maas[10] has shown that spiking neural nets can achieve computational performance far superior to that of McCulloch-Pitts neural nets.[11]

These results must be encouraging for theoreticians, but they remain very much theoretical. The models are inspired by neural anatomy; however, very few simulate anatomic structures in detail. More relevant results would be those which map to particular recursive structures in the human brain. If these structures could be shown to exhibit powers transcending mere self-motion (preferably rising towards the psychological realm) the results would be of value to the current critique. We will see below that a brain structure essential to the function of memory does exhibit such powers.

One machine which Maas has modeled on spiking neural nets is a kind of "random access memory."[12] Neural net memory structures can be highly recursive, and this suggests that bodily memory structures might also contain recursive components. As it happens, one such recursive memory structure is well known. It is located within the hippocampus, an organ situated at the crossroads of sensory pathways in the brain.

The hippocampus is not an easy structure to visualize. For this reason several anatomical images will be presented among the paragraphs to follow. The images are ordered so as to guide the reader's eye down to the hippocampus, and to expose the recursive structure within.

Fig. 6.1
Limbic system[13]

This cutaway view displays some of the brain's deep limbic system structures, as seen through the temporal lobe from a viewpoint above the left temple. The two lobes of the hippocampal formation lie below the centrally-located thalamus. Distant brain areas connect to the hippocampus through two fiber bundles visible in the illustration: the cingulate gyrus and the fornix. The cingulate gyrus contains most of the hippocampus' afferent (input) fibers. The fornix contains most of the efferent (output) fibers.

Fig. 6.2
Hippocampal formation[14]

Figure 6.1 is inset within Figure 6.2, at upper left. Figure 6.2 isolates the hippocampal formation (shaded in inset).
This cutaway reveals the folded tissues of the hippocampus. The dentate gyrus is the interior fold. The cornu ammonis is the exterior fold. The cornu ammonis is not labeled in Figure 6.2, but is marked in another cutaway view, Figure 6.3, below.

Fig. 6.3
The dentate gyrus is labeled "DG." The cornu ammonis is labeled "CA."[15]

This exterior fold, the cornu ammonis, is the main site of memory processing in the hippocampus. An overview of its supposed function will follow these figures.

Fig. 6.4
Photograph of exposed hippocampus[16]

In Figure 6.4 the hippocampus is rotated 180 degrees relative to Figure 6.3. The bar at lower right is 6.5 mm, for scale.

The hippocampus is common to many animals. Most hippocampal experiments have been performed on rats. Subsequent diagrams are of rat hippocampal regions, all of which have close analogues in the human hippocampus.

Fig. 6.5
Rat hippocampus[17]

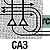
In Figure 6.5 the cornu ammonis is again labeled "CA." Two regions are marked: "CA1" and "CA3." Also, the dentate gyrus, at bottom, is once again labeled "DG." Major nerve pathways through these structures are illustrated by individual neurons. Arrows indicate the general flow of information.

Fig. 6.6
CA1 and CA3 regions are inverted in humans, relative to rats.[18]

Fig. 6.7
Schematic of connections and information flow[19]

Figure 6.7 magnifies Figure 6.5 with a more detailed schematic of connections and information flow in the hippocampus. Note the looping structure marked as "Recurrent collateral" in the CA3 region at left. Recurrent collaterals occur where nerve output fibers (axons) circle back upon the nerve input fibers (dendrites) of neighboring cell bodies. Collaterals are the synaptic connections between axons and dendrites. The recurrent collateral in Figure 6.7 is of special interest: it is a known example of a recursive structure in the brain. We can trace the flow of information through the hippocampus, marking the recursion where it occurs:

In Figure 6.7 information flows through the perforant path (1) to the dentate gyrus and the CA3 region. The dentate gyrus also projects information through the mossy fibers (2) to the CA3 region. Recurrent collaterals cycle inputs within the CA3 region. (This is the recursion.) Thereafter the CA3 region projects through the Schaeffer collateral (3) to the CA1 region. The CA1 region projects to the subiculum (4) and on to other cortical areas.

The recursion in region CA3 figures more prominently in Edmund Rolls' network schematic, Figure 6.8:

Fig. 6.8
Hippocampal network schematic[20]

In Figure 6.8 the block diagram at left shows the overall information flow between regions. The symbolic diagram at right highlights recurrent collaterals ("rc") of the CA3 region, which stand out by virtue of their distinctive looping structure.

The diagrams in Figure 6.8 clarify Figure 6.7. They showcase the hippocampus' recursive information flow. Afferent (input) connections are shown as solid lines. Efferent (output) connections are shown as dashed lines. At right, the more detailed symbolic diagram shows dendrites as thick lines, and axons as thin. "rc" indicates that recurrent axons loop their collaterals back onto dendrites within the CA3 region — the site of recursion.

The hippocampus is known to form "episodic memories": memories of episodes, or events.[21] The sensations impinging on the brain at the time of an event are associated together, by the hippocampus, into that one event memory. When that event is recalled through the hippocampus, those sensations emerge as a unit to reconstruct the event in the imagination.

The role of the hippocampus in storing and recalling events has been a subject of investigation since the 1950s.[22] More recently the CA3 region has been singled out for especially intense study. The CA3 region is the portion of the hippocampus which contains a high number of recurrent collaterals, as noted in Figures 6.7 and 6.8. As a group, these "coiled" neurons produce outputs which contribute to their own inputs. And under the right conditions recurrent collaterals can propagate nerve impulses in self-sustaining loops. This does seem to occur in the CA3 region. It's a biological form of recursion, with computational properties essential to the formation of episodic memories.

The computational properties of greatest interest are those of an "autoassociator." This device is just a neural net which has been completely permeated by its recurrent collaterals.

Fig. 6.9
An autoassociator of the type theorized for the CA3 region[23]

Figure 6.9 diagrams an abstract autoassociator. The sequence of changes which are thought to occur during episodic memory formation in the CA3 region can be read from the diagram in this way:[24]

External input sensations (e_i) excite dendrites (thick lines) to produce simultaneous electrical activation (h_i) on a group of neurons. In turn, those activated neurons' cell bodies (triangles) fire outputs (r_i). The recurrent collaterals (r'_j) of these outputs strengthen synaptic connections (w_ij) on just the excited dendrites in the group. This cycle continues for the duration of the external input. After a few cycles the memory pattern is stored, as a single remembered event, in the strengthened connections.

Edmund Rolls and Alessandro Treves have modeled the neural net thought to exist within the hippocampus.[25] Here are some of their experimental results:

The simulated hippocampus was able to store all presented event memory patterns.[26]
It recalled those memories reliably when prompted with a small "cue" memory stimulus. Memory recall was perfect when the cue contained as little as 40% of each pattern.[27]
Recall failed completely when the recurrent collaterals of the CA3 region were disabled.[28]
The number of event memories which the simulated hippocampus could store was proportional to the number of recurrent collateral synapses per CA3 cell.[29]
The estimated number of storable event memories (36,000 for the rat)[30] is consistent with the clinical theory that the CA3 region stores memories for a brief time only. (It is thought that the hippocampus transfers older memories to the neocortex as newer ones are acquired.)[31]

Rolls characterizes the results:

The immediate interest of a simulation like this is, of course, that it works. A network with the connectivity and general structure of a specific brain area, the hippocampus, presented with inputs which produce a similar sparseness of activity to that found there, using a learning algorithm which is related to one which is known to operate in this area, and given the same limited opportunity to learn a large number of memories (one presentation per pattern) can perform a function similar to that which the area appears to perform in the brain. We must, surely, feel that progress is being made in understanding how the hippocampus works as part of the brain's system for memory formation.[32]

Other recent experiments support these findings.[33],[34] So we can infer with some confidence that the body relies heavily upon recursion when storing and recalling memories of events.

This result, and the results discussed previously, must now be laid out alongside Proclus' propositions so that we may conclude this rambling critique.

next Chapter 7: Mortality

Chapter 6 Endnotes

[1] John C. Shepherdson, "Mechanisms for Computing Over Arbitrary Structures," The Universal Turing Machine: A Half-Century Survey 581-601.

[2] Shepherdson 597. Quoting:

"For every mechanism satisfying [Gandy's four 'Principles of Mechanisms'] there is a parallel Turing machine which is equivalent to it on all interpretations on which it is determinate."

[3] McCulloch and Pitt's original 1943 article, "A Logical Calculus of the Ideas Immanent in Nervous Activity," is reprinted in Warren S. McCulloch, Embodiments of Mind (Cambridge, Massachusetts: The MIT Press, 1965) 19-39.

[4] McCulloch 22. See also Chapter 17, note 42.

[5] Hava T. Siegelmann and Eduardo D. Sontag, "On the Computational Power of Neural Nets," Journal of Computer and System Sciences, 50:1 (1995): 132-50.

[6] The "spiking" behavior is codified by complex threshold and response functions. See also Chapter 17, note 42.

[7] Wolfgang Maas, "Lower Bounds for the Computational Power of Networks of Spiking Neurons," Neural Computation 8:1 (1996): 1-40.

[8] Finite automaton (finite state machine): "an abstract machine consisting of a set of states (including the initial state), a set of input events, a set of output events, and a state transition function. The function takes the current state and an input event and returns the new set of output events and the next state. Some states may be designated as 'terminal states'. The state machine can also be viewed as a function which maps an ordered sequence of input events into a corresponding sequence of (sets of) output events." Source: Free On-line Dictionary of Computing.

[9] Random access memory: "the most common computer memory which can be used by programs to perform necessary tasks while the computer is on; an integrated circuit memory chip allows information to be stored or accessed in any order and all storage locations are equally accessible." Source: WordNet 1.6.

[10] Wolfgang Maas, "Networks of Spiking Neurons: The Third Generation of Neural Network Models," Neural Networks 10:9 (1997): 1659-71.

[11] The particular example chosen used a single spiking neuron to perform a computation which would require hundreds of McCulloch-Pitts neurons.

[12] Maas, "Lower Bounds for the Computational Power of Networks of Spiking Neurons," 30 -31.

[13] Walter J. Hendelman, Student's Atlas of Neuroanatomy (Philadelphia: W. B. Saunders, 1994) 181.

[14] Hendelman 189.

[15] Peter McLeod, Kim Plunkett, and Edmund T. Rolls, Introduction to Connectionist Modelling of Cognitive Processes (Oxford: Oxford University Press, 1998) 279.

[16] Henri M. Duvernoy, The Human Hippocampus, 2^nd ed. (New York: Springer, 1997)15.

[17] Juaquin M . Fuster, Memory in the Cerebral Cortex: An Empirical Approach to Neural Networks in the Human and Nonhuman Primate (Cambridge, Massachusetts: The MIT Press, 1995) 26.

[18] Duvernoy 19.

[19] McLeod, Plunkett, and Rolls 282. Quoting the original caption:

"A schematic representation of connections within the hippocampus. Input comes through the perforant path (1) which synapses with the dendrites of the dentate granule cells and also with the apical dendrites of the CA3 pyramidal cells. The dentate granule cells project via the mossy fibres (2) to the CA3 pyramidal cells. The recurrent collateral system of the CA3 cells is indicated by the single axon labelled Recurrent collateral. The CA3 pyramidal cells project via the Schaeffer collateral (3) to the CA1 pyramidal cells, which in turn have connections (4) via the subiculum back to other cortical areas."

[20] McLeod, Plunkett, and Rolls 284. Quoting the original caption:

"Forward connections (solid lines) from areas of cerebral association neocortex via the parahippocampal gyrus and perihinal cortex, and the entorhinal cortex, to the hippocampus. Backprojections (dashed lines) via the parahippocampal gyrus to the neocortex. There is great convergence in the forward connections down to the single network in the CA3 pyramidal cells and great divergence again in the backprojections. Left: block diagram. Right: more detailed representation of some of the principal excitatory neurons in the pathways. [triangle] represents pyramidal cell bodies; [circle] represents dentate granule cells. The thick lines above the cell bodies represent the dendrites; the thinner lines with arrow heads the axons. Abbreviations: DG: dentate granule cells. mf: mossy fibres. PHG: parahippocampal gyrus. pp: perforant path. rc: recurrent collateral of the CA3 hippocampal pyramidal cells."

[21] For an introductory overview of the principles of neural memory formation, and the role of the hippocampus in the acquisition of episodic memories, see Fuster 23-46. For photographs of long-term memory structures, see a dissection of memory structures in the sheep brain.

[22] For a very readable history of twentieth-century memory research, see Brenda Milner, Larry R. Squire, and Eric R. Kandel, "Cognitive Neuroscience and the Study of Memory," Neuron 20:3 (1998): 445-68.

[23] Edmund T. Rolls and Alessandro Treves, Neural Networks and Brain Function (Oxford: Oxford University Press, 1998) 43.

[24] A good introduction to autoassociators can be found in McLeod, Plunkett, and Rolls 72-95.

[25] Rolls and Treves 95-135. A summary of that analysis is presented as part of an introductory course on neural net theory in McLeod, Plunkett and Rolls 279-92.

[26] McLeod, Plunkett and Rolls 289.

[27] McLeod, Plunkett and Rolls 289.

[28] McLeod, Plunkett and Rolls 290.

[29] Rolls and Treves 113.

[30] Rolls and Treves 113.

[31] Rolls and Treves 122-29. For biochemical details, see Ivan Izquierdo and Jorge H. Medina, "Memory Formation: The Sequence of Biochemical Events in the Hippocampus and Its Connection to Activity in Other Brain Structures," Neurobiology of Learning and Memory, 68:3 (1997): 285-316. For a very recent (2000) proposed linkage of hippocampal and cortical memory systems, see Edmund T. Rolls, "Hippocampo-Cortical and Cortico-Cortical Backprojections," Hippocampus, 10:4 (2000): 380-88.

[32] McLeod, Plunkett and Rolls 289-90.

[33] Some supplementary theories on overall hippocampal function can be found in L. R. Squire, "Memory and the Hippocampus: A Synthesis From Findings With Rats, Monkeys, and Humans," Psychological Review 99:2 (1992): 195-231; James L. McClelland and Nigel H. Goddard, "Considerations Arising From a Complementary Learning Systems Perspective on Hippocampus and Neocortex," Hippocampus 6:6 (1996): 654-65; Mark Moll and Risto Miikkulainen, "Convergence-Zone Episodic Memory: Analysis and Simulations," Neural Networks 10:6 (1997): 1017-36; Richard Granger, et al., "Distinct Memory Circuits Composing the Hippocampal Region," Hippocampus 6:6 (1996): 567-78.

[34] Some theories on the hippocampus' role in storage and retrieval (including dreamtime retrieval) of temporal sequences of episodic memories can be found in William B. Levy, "A Sequence Predicting CA3 Is a Flexible Associator That Learns and Uses Context to Solve Hippocampal-Like Tasks." Hippocampus 6:6 (1996): 579; D. A. August and William B. Levy, "Spontaneous Replay of Temporally Compressed Sequences by a Hippocampal Network Model," Computational Neuroscience: Trends in Research, 1997, ed. James M. Bower (New York: Plenum Press, 1997) 231-36; Yu-Lin Qin et al.. "Memory in Hippocampal-Neocortical Ensembles," Philosophical Transactions of the Royal Society of London: Series B 352:1360 (1997): 1525-33; J. L. Kavanau, "Memory, Sleep and the Evolution of Mechanisms of Synaptic Efficacy Maintenance," Neuroscience 79:1 (1997): 7-44.