|
Chapter 15 Noetic Reduction |
|
There is another property of existential
passage which deserves mention. I'll call it "noetic reduction,"
with a definition to come. This corollary property
derives from the following observation:
Under the proposed tenets of
Metaphysics by Default merged passages would be common, and of course more persons would enter each merged passage than would leave it.
For example a two-to-one passage would begin with two persons and end with only
one. A three-to-one passage would begin with three and end also
with one. As a rule, every merged passage is thought to end by dropping the number
of participating persons down to one.
Now,
subjectively, the passage participants would be ignorant of this decrease in
their number. But objectively we can see that a decrease should
occur with every merger.
In Chapter 11 we saw that an apparent shrinkage of the population was
actually balanced by ex nihilo passages. That
result still holds true, for the overall
population. But this decrease in the number of passage participants would
produce a cumulative effect on any particular group
of individuals. Over time, generations within that
group would cascade through a series of passages; each generation encountering a decrease in number as members of the group merge into fewer recipients.
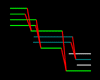
Figure 15.1 illustrates a decrease due to merged passages. Three generations are represented.
The first generation is at upper left, the
second at center, and the third at lower right:[1]
|
|
Colors on the
timelines mark off distinct population groups. We can trace like-colored lines to see where each group's population has decreased. For example, the blue-line group shows a
decrease from the second generation to the third, with two members of the second-generation group merging into a single member of the third. Green lines mark off a different group, which undergoes a separate,
multi-generation decrease. Here all four members of the first-generation group merge
into two members of the second. That second-generation group merges in turn into a single individual, in the third generation.
Although these
passage participants cannot know it, they are being "packed together,"
and rapidly.
In Figure 15.1 the green multi-generation decrease is that of four persons passing through two generations of
mergers into a single final recipient. That one recipient now continues
the life experience of that group's original four members. Mergers have here "reduced" those four persons down to one.
(Here I am drawing upon a meaning of reduction that equates with
the "removal of volatiles," as when a dilute solution is boiled to remove water.)
In the
metaphysics, what is reduced is not the overall population per se. For the sake of mathematical simplicity we have assumed
back in Chapter 13 that the overall population remains near some equilibrium
number, and we continue to hold by that assumption. This is reiterated
visually in Figure 15.1, wherein each generation is assigned an unvarying
population of four individuals.
So the reduction
does not apply to the overall population. Rather, it applies to a
given group's starting population. When we track that particular group over successive generations we see that the
number of recipients inheriting that group's passages tends always towards
one. The group members' personal identities are being coalesced progressively
closer to a single common identity as each generation of merged passages reduces
the number of individuals remaining from the group's original population.
The mergers are
forcing out the "space" between distinct living minds, joining their
subjectivities together into a progressively smaller number of individuals: down
to the final reduction of one. When the group
is reduced to one individual, no further reduction of that group can occur; as one is the minimum number of participants, n, in any n-to-one
passage.[2]
Taking a page
from Teilhard de Chardin, we might say that the group's starting population
constitutes a "noosphere"[3] of independent minds. As
merged passages force out the space between those minds, and reduce the group,
that noosphere shrinks. When the number of individuals reaches one, the
noosphere has reduced to its smallest possible size. The phrase
"noetic reduction" can serve as a moniker for this coalescent
process.
So, what is the
per-generation percentage decrease due to merged passage (i.e., the noetic
reduction percentage)?
To get
this percentage we will need to find two factors which will be multiplied
together in the result. The factors are:
To get (1), let's consider the following:
As we can see, it is the number of persons, n,
participating in the n-to-one merger which
determines the percentage decrease. The percentage decrease for n-to-one merger follows this rule:
Percentage
decrease = ((n-1)/n) x 100%
This takes care of (1). And we already
have (2), from Chapter 13 (verified in
Appendix A):
pn = 0.25 n x (1/2)n-1
We multiply these two factors together to
get a formula for the group's per-generation percentage decrease. And
then we sum this formula over all possible values of n, to get the group's total per-generation percentage decrease.
Here is the power series sum, without simplification.[4] The noetic reduction percentage, per generation, is:
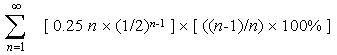 This sum is proved to be of the form: a x / (1-x)2. Here a = 25% and x = 1/2. The result:
Specifically, we
can calculate the number of generations (nGEN) for
an arbitrary population (x) to reduce to some
smaller population (y), given the decimal percentage
of noetic reduction per generation (dNR). The formula for this calculation can be derived
in a few steps:
In one
generation noetic reduction decreases a population x
down to a population y. Solving for y:
y = x - dNR x
y = x - 0.5
x
y = x(0.5)
The process continues for nGEN generations. Over those nGEN
generations, population x is multiplied by 0.5, nGEN times, in order to obtain the final reduced
population y. Solving now for nGEN:
y =
x
(0.5)
nGEN
(0.5)
nGEN =
y /
x
nGEN = ln (
y / x ) / ln (0.5) Now we have a formula for nGEN:
nGEN = ln (
y / x ) / ln (0.5)
We can use this formula to find the number
of generations required to reduce one arbitrary population to another. For
example: We begin with a starting population roughly that of the United States,
where:
x = 300,000,000
And we'd like to know how long it would
take for a population of this size to reduce to the size of a small country town, where:
y = 3,000 Applying our formula for nGEN:
nGEN = ln ( 3,000 / 300,000,000 ) / ln (0.5)
= ln (0.00001) / ln (0.5)
nGEN = 17 generations, or roughly 510 years.
For a more dramatic example, we could ask,
"How long would it take for the world's current human population to reduce
down to a single individual?"
Here we'll take x as 6 billion. y
we'll take as 1.5, rather than 1, because noetic reduction is
"step-wise." When the population is calculated theoretically as
a fractional value of less than 1.5, it should in reality "step down" to
1 exactly, because fractional personal identities are not thought to exist.[7]
So, with these
values of
x and y, we
get the following
nGEN:
nGEN = ln (1.5 / 6,000,000,000 ) / ln (0.5)
= ln (2.5
x 10 -10) / ln (0.5)
nGEN = 32 generations, or roughly 960 years.
|
|
Chapter 15 Endnotes |
|
[1] Actual generations overlap more than indicated by the timelines of
Figure 15.1. Here as elsewhere in the essay, generations are temporally
separated so as to improve the visual clarity of the timeline illustrations.
Chapter 16 will certify that this convention does not alter the mathematics. [2] No "partial" or "fractional" personal identity
seems plausible. For this reason we can suppose that a single identity
will pass to a single identity, indefinitely; with no further reduction.
As noted in Chapter 11, split passages may exist, but the practical difficulty of
synchronization would appear to be considerable. And for this reason split
passages are thought to be, at best, extremely rare. Consequently their
negligible probabilities are not factored into these equations, or into any
equations of Metaphysics by Default.
[3] This author takes no strong position with regard to the truest
meaning or teleology of the word "noosphere", only noting that the
vision of "mind-space" which it establishes can serve as a well-known
point of departure for the hike to noetic reduction. For an introduction
to noosphere — and other concepts in the philosophy of Teilhard de Chardin
— see Pierre Teilhard de Chardin, Let Me
Explain, trans. Rene Hague, et al. (London: Collins, 1970). Hague
provides a definition of Teilhard de Chardin's noosphere on pages 17-18.
Quoting:
"Noosphere (from Noos, mind): 'The terrestrial sphere of thinking substance.' It is the thinking envelope woven around the earth, above the biosphere, and made up by the totality of mankind. Its reality is already existing, and its density is constantly increasing through the rise in the human population, its inter-relations, and its spiritual quality."By this definition we may infer that noosphere is to be understood as emerging through the social interaction of individual minds. Teilhard de Chardin's imagery sometimes suggests a noosphere which transgresses the boundaries of personal identity, but I think a conservative reading of the definition reconciles noosphere to personal identity as the latter concept has been presented in this essay.
[4] The formula for this sum can be simplified, but I
leave all the original factors of (1) and (2) in this statement of the formula,
so as to make the derivation clear. If we simplify and convert to decimal probability we get: 0.25 n x (1/2)n. a = 0.25, x = 1/2.
[5] Provided, again, that the overall population is stable over time
near some equilibrium number.
[6] This result receives indirect support from the
mathematics of Chapter 14. In Chapter 14 we found ex nihilo passage to be
as likely as participated passage. In consequence, only half of each newborn
generation is thought to inherit passages from the previous. The inference is that the previous
generation has passed to a population half its size.
[7] That being said, there is less than one generation in difference
between a calculation of y = 1 and
y = 1.5.
[8] As a corollary, we can note that the individual recipient
of the whole-species population group has won the title against long odds. In the
example cited, the odds were 6 billion to 1. All other contemporaneous passage recipients
have
inherited younger population groups: these groups are comprised of members
whose multi-generational ages are less than 960 years. (Again, granted population
stability near 6 billion, and with the understanding that the reduction rate is only a probabilistic
average.) |
Copyright © 1999
Wayne Stewart
Last update 4/19/11