|
Chapter 16 Summary of Mathematical Results | ||||||||||||||||||||||||||||||||
|
Chapters 13-15 have derived three aggregate mathematical results. I should emphasize that these results can apply only to populations meeting the conditions assumed at the start of Chapter 13
— the assumption of population stability being especially critical.[1]
Summarizing the
results in the order of their derivation:
Question: We have seen in Chapter 13 that unitary, one-to-one passage has an absolute
experienced probability of 0.25, or 25%. We interpret this as meaning that
a person would have a 25% chance of experiencing a unitary passage.
All other
n-to-one passage types add up to a 75% probability. Since all other n-to-one passages are merged passages, a person should have a 75%
chance of experiencing a merged passage.
The ratio, 75:25,
is just 3:1.
And so the
experienced ratio of merged to unitary passage would be 3:1. Under normal circumstances, a passage
participant would be three times as likely to encounter a merged passage as a
unitary passage.
Question: The rule for predicting the occurrence of n ex nihilo passages (pex n) is the same as the rule for determining the
probability of each n-to-one passage type (pn). We have seen in Chapter 14 that these probabilities are
equivalent:
pn = pex n = (1/2)n-1 { n = 1 to infinity }
Since the rules are the same, the
probabilities are the same. The probability that a
newborn would experience an ex nihilo passage is the
same as the probability that the newborn would be the recipient of an n-to-one passage. And so newborns would be equally
likely to experience ex nihilo passage, as not.
Question: The noetic reduction per generation for a
particular group is calculated as the sum:
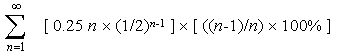
We have seen in Chapter 15 that this sum is 50%. And so with
the passing of each generation a given population would undergo noetic reduction
into a population just half its original size.
The cumulative
effect would appear to be capable of reducing a whole-species population group
down to a single individual, over the course of several hundred years.
These two sets of
results are listed side-by-side in Table 16.1 below. Each row in the
table presents the calculated decimal probability for a different passage type.
The final row presents the aggregate merged-to-unitary ratio:
|
||||||||||||||||||||||||||||||||
Table 16.1
|
||||||||||||||||||||||||||||||||
|
The formal and informal results match
well. This satisfies the purely mathematical requirements of the
philosophy.
Beyond
this, a visual calculation of the system dynamics
can give additional confirmation. Interactive visuals can engage the reader at each controlled step. For these reasons
I attach a "Monte Carlo program" below. It performs interactive visual
calculations of the three aggregate results reviewed above.
|
||||||||||||||||||||||||||||||||
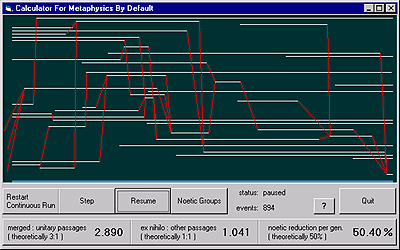
Appendix B — calculator for Metaphysics by Default. The calculator of Appendix B sets up a series of random population events. Once the events have been generated, the program "walks through" the events, progressing along a simulated timeline. At each time increment the program records the passage events specified by the conditions of that moment. The program then updates the three aggregates derived previously: the ratio of merged to unitary passage, the ratio of ex nihilo to all other passages, and the noetic reduction percentage. A ReadMe file guides installation.
A question mark button on the display panel opens operating instructions. As the program
runs, its outputs settle near the theoretical values derived informally in
Chapters 13-15, and verified formally in Appendix A. The program contains no explicit rule which forces
its calculated results to match the theoretical results. Instead the
cumulative events conform naturally to a probability distribution similar to that found in the
formal and informal probability arguments. For this reason the program
produces aggregate values in accord with mathematical prediction.
Sample Monte
Carlo program results, compiled from two different applications,[2] are printed alongside previous results in
a combined table, Table 16.2, below. The close agreement of all three sets of results gives
us greater assurance of the soundness of all three techniques.
| ||||||||||||||||||||||||||||||||
Table 16.2
|
||||||||||||||||||||||||||||||||
|
next Chapter 17: Application to Other Species | ||||||||||||||||||||||||||||||||
|
Chapter 16 Endnotes |
||||||||||||||||||||||||||||||||
|
[1] A sustained population
increase would
result in the following qualitative changes to the three aggregate results
summarized in this chapter:
A sustained population decrease would produce metaphysical changes opposite those attendant
a population increase.
[2] The ex nihilo and merged/unitary Monte
Carlo ratios were obtained by a Visual Basic 5 program over the course of
1,000,000 simulated events.
Appendix B;
Appendix C.
All other Monte Carlo results were obtained by a
Macintosh Thin C program over the course of 1,000,007 simulated events. Appendix D.
[3] Please refer to note 2 for details of the Monte Carlo program
results.
|
Copyright © 1999
Wayne Stewart
Last update 4/19/11