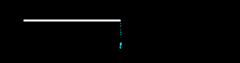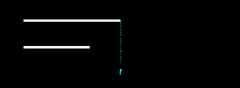Chapter 14. Ex Nihilo Probability

Home - Welcome
Forum *(new)*
Lectures
1	A Word of Encouragement
2	Dar al-Hikma
3	Proclus' Elements
4	Reversion in the Corporeal
5	Mathematical Recursion
6	Episodic Memory
7	Mortality
7s	Classical Mortality Arguments
8	Personal Identity 1 2 3 4
9	Existential Passage 1 2 3
10	Precedent at Dar al-Hikma
10s	Images of Dar al-Hikma
11	Passage Types
12	A Metaphysical Grammar
13	Merger Probability
14	Ex Nihilo Probability
15	Noetic Reduction
16	Summary of Mathematical Results
17	Application to Other Species 1 2 3 4
18	Potential Benefits
19	A Dedication
Appendices
Works Cited
E-mail the author. E-mail the webmaster.
.

Chapter 14
Ex Nihilo Probability

In the previous chapter we determined that a person encountering existential passage would be three times as likely to experience a merged passage as a unitary passage. Now we can turn our attention to the recipient of the existential passage.

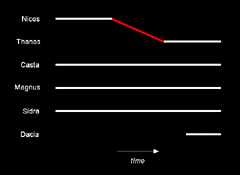
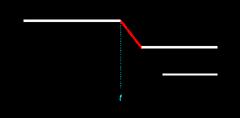
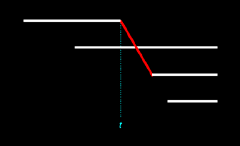
Not all newborns are thought to receive passages under Metaphysics by Default. As we've seen previously in Figure 11.6, a newborn can appear at a time when no passage participant (i.e., no ending terminus) is available.

Figure 11.6 is printed again below as Figure 14.1. In this figure Dacia (at bottom) receives no existential passage:

Fig. 14.1
Ex nihilo passage

This situation was defined in Chapter 11 as ex nihilo passage, passage out of nothing. This is a passage event which involves no transmigrating participant: it is "unparticipated" in that sense.

Continuing our mathematical analysis from the previous chapter, we now ask:

How likely is ex nihilo passage, relative to participated passage?

We can use the same probability technique developed in the previous chapter to find an informal answer to this new question. As before, a formal answer does also exist. The formal derivation is located in Appendix A.

We set up our informal solution to this new mathematical problem by considering the most basic ex nihilo passage scenario.

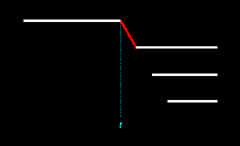
The simplest scenario is this: a person has been born into a simple cosmos, and thereafter has passed away at some time t. We "freeze" that person's timeline in Figure 14.2. We'll assume that it cannot be altered, and that for now it represents the only life that has existed in the cosmos.

Fig. 14.2
One ex nihilo birth

In figure 14.2 we see that this person, being the only person extant in his cosmos, must have been born as an ex nihilo passage. This is certain. We will denote this probability as p_ex1, thus:

p_ex1 = 1

where p_{ex n}stands for the relative probability of n persons being born into ex nihilo passage.

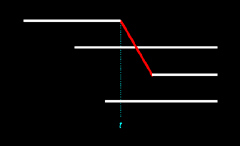
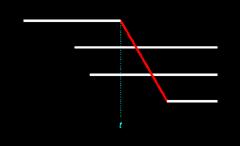
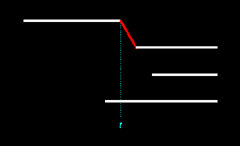
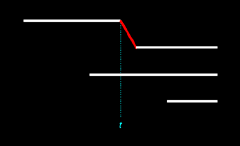
Now we add a second person, a potential recipient of that first person's existential passage. The timing of the birth of this second person we will consider to be random. This potential recipient may be born at any time, either before or after time t, unpredictably. The two possible types of outcomes are illustrated in the following two figures:

Fig. 14.3

Fig. 14.4

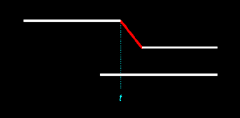
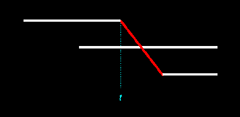
In Figure 14.3 we see that both of the illustrated births are ex nihilo passages. However, this is not the case in Figure 14.4, wherein only one birth is an ex nihilo passage. Since each of these two outcomes is equally likely, the probability that all births will be ex nihilo passages is here 1/2, or 0.5. We denote this probability as p_ex2:

p_ex2 = 0.5

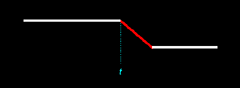
What if we add a third birth to the scenario? We can create another set of figures to determine the probability that all three births will be ex nihilo passages. Again, the random births we've added may occur at any time, either before or after time t. Four outcomes are now possible:

Fig. 14.5

Fig. 14.6

Fig. 14.7

Fig. 14.8

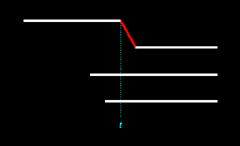
Only in Figure 14.5 are all three births ex nihilo passages. Since each of the four outcomes is equally likely, the probability that all births will be ex nihilo passages is here 1/4, or 0.25.

p_ex3 = 0.25

What if we add a fourth birth to the scenario? We can create another set of figures to determine the probability that all four births will be ex nihilo passages. Again, the random births we've added may occur at any time, either before or after time t. Eight outcomes are now possible:

Fig. 14.9

Fig. 14.10

Fig. 14.11

Fig. 14.12

Fig. 14.13

Fig. 14.14

Fig. 14.15

Fig. 14.16

Only in Figure 14.9 are all four births ex nihilo passages. And so the probability that all four births will be ex nihilo passages is here 1/8, or 0.125.

p_ex4 = 0.125

A progression of relative probabilities for each n-tuple group of ex nihilo passages is emerging, according to the rule:

p_{ex n} = (1/2)^n-1 { n = 1 to infinity }

where, again, n is the number of newborns experiencing ex nihilo passage.

And now the informal derivation of the overall ex nihilo probability is almost complete.

Let's recall from Chapter 13 our very first attempt at a probability rule. We came up with a rule for determining the relative probability of each n-to-one passage type:

p_n = (1/2)^n-1 { n = 1 to infinity }

This rule is identical to the relative probability rule predicting the occurrence of n ex nihilo passages:

p_{ex n} = (1/2)^n-1 { n = 1 to infinity }

Since the rules are the same, the probabilities are the same. And so we see that the probability that a newborn would experience an ex nihilo passage is the same as the probability that the newborn would be the recipient of a passage. It follows that a newborn would be equally likely to experience ex nihilo passage, as not.

Stated as a ratio: Newborns' experienced ratio of ex nihilo passage, relative to participated passage, would be 1:1.

From the probability results derived so far, we can also generate the mathematics of a corollary property, "noetic reduction." This property will be defined, and its mathematics determined, in the next chapter.

next Chapter 15: Noetic Reduction